Using Binomial Probability Calculators to Clarify the Strength of Telepathy Test Results

There is a huge body of literature collectively proving the reality of extrasensory perception (ESP), also called telepathy. Unfortunately much of the literature is written by writers who failed to effectively communicate how improbable it is the results they reported could be explained by chance. There is no excuse for an ESP investigator to fail to clearly explain the improbability of very improbable results that he got. Such an investigator is already climbing a steep hill that results from the senseless stubbornness of people who refuse to accept observational results they cannot explain under their presumptions. If the investigator wants to convince people, he needs to clearly communicate exactly how improbable are the improbable results he  achieved. 

For example, if you are an ESP experimenter who had people guess the colors of randomly selected playing cards, and you got a result of 496 successes our of 830 trials, it is not at all sufficient to merely point out that such a result is 81 successes more than expected by chance.  A reader may not realize that such a result should be expected on less than 1 in a million trials. 

Luckily nowadays there is a type of online tool you can use to help clarify what the probability was when extremely unlikely results were achieved.  The tool is called a binomial probability calculator.  The tool is easy to use, and typically involves three inputs: 

(1) The number of trials.

(2) The chance of success on any trial.

(3) How many successes occurred. 

Using a binomial probability calculator, you can type in all of these numbers, and press a button, typically marked "Calculate" or "Compute." You then will be given some results that clarify how likely such a result was. 

You can find such calculators by typing "binomial probability calculator" into a search engine. The first result that will come up is the Stat Trek binomial probability calculator available here.  This calculator works well for calculating improbabilities that are not too small. But the Stat Trek binomial probability calculator has the imperfection that it reports extremely low probabilities as being zero. 

I can give an example. Let us imagine an ESP test in which people are asked to guess the color of 830 playing cards randomly chosen at some interval in a shuffled deck in another room. Suppose there are 472 correct guesses. If you put the corresponding numbers into the Stat Trek binomial probability calculator, you will get the result shown below:

On the last row the calculator shows the chance of getting a result greater than or equal to 472 is only about .00004.  But imagine if you change the "number of successes" input to be 496, which was the actual result in an ESP test reported here. Now, the Stat Trek calculator will incorrectly claim that there was a zero chance of such a result:

This is not quite right, because the probability of such a result is very low, but not zero. To get the correct result, you will need to use a different binomial probability calculator, such as the one at www.wolfframalpha.com. 

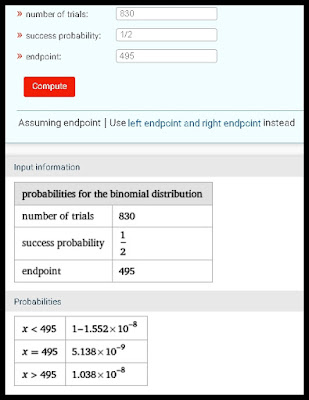
The binomial probability calculator at that site can be found here. The calculator has a rather confusing appearance. Rather than an input labeled as "number of successes," we have an input confusingly labeled as "endpoint."  When using the calculator, it is best to put in the number of successes in the "endpoint" slot, subtracting 1 from the actual number of successes. Here is the result of using the calculator with the example above:

Now we have (in the last row) a page correctly telling us about the unlikelihood of the reported result. (If you don't understand the way the calculator expresses these very low probabilities, look up the topic of scientific notation, finding a page like this one.) In an ESP test in which people are asked to guess the color of 830 playing cards randomly chosen in a shuffled deck in another room, at particular intervals, the chance of getting 495 or more successful guesses is 1 in 1.038 times 10 to the eighth power, about 1 in 100 million. This is exactly the result reported in row 1 of the table you can see using the link here. The table is shown below:

The results were published in 1927 by Professor G. H. Estabrooks, professor of psychology at Colgate University. The technique used to get these results is described at the link here and in the next several pages you can read using that link. The results were produced using a variety of subjects, with the tested subject and the card drawer in adjacent rooms that were separated by a closed door. A signal that it was time to guess the suit or the color of the card was sent by a telegraph-like apparatus. 

The tests above show a kind of "fatigue" effect, in which the guesses are more likely to be true at the beginning than the end. I am not at all surprised to read of such a result.  In my post "How to Test ESP or Telepathy Using Your Friends or Family Members," I recommend doing very short tests allowing three or four guesses, over multiple days, without the test ever lasting more than a few minutes. Such a method is best to avoid the "fatigue" effect shown above. I have sometimes got great success in informal brief tests of ESP using family members, which I describe in my post here. 

Here is the result I get using the www.wolfframalpha.com binomial probability calculator to calculate the first row of Table 2 shown in the visual above. 

 

We have the calculation that when guessing the suits (diamonds, spades, clubs or hearts) of 830 shuffled cards, the probability of getting more than 255 successes is .000083. 

The two probabilities are independent; in other words, the probability of getting the first result by chance does not affect the probability of getting the second result by chance. A chief rule of probability calculation is that when you have two independent results with a probability of x and y, the probability of getting both of them (in two consecutive trials) is x times y.  For example, the probability of drawing the ace of spades twice in a row from a newly shuffled full deck is 1 in 52 times 1 in 52, or 1 in 2704. Using this rule we can calculate that the chance of getting both the result in the first row of Table 1 shown above and the result in the first row of Table 2 shown above is roughly 1 in 100 million multiplied by .000083, which equals .0000000000008 or roughly 1 in a trillion (1 in 1,000,000,000,000). That's a result we never would expect to get by chance in any of the formal academic ESP tests ever done, since the number of tests done is relatively small, much less than 1 million. It's a level of success we would not expect to get from mere chance even once if every person on Earth was tested for their telepathy ability five different times.

The results in the table above are by not by any means the most impressive ESP tests ever produced. Vastly more impressive results are reported here and here and here. The laboratory evidence for ESP is overwhelming, and binomial probability calculators help to clarify how strong such evidence is.