The
Miller-Urey experiment was an experiment done in the 1950's which was
claimed to be a big advance relating to the origin of life. The
coverage of this experiment in the scientific mainstream is one of
the most egregious cases of hype, erroneous information and faulty analysis to be found anywhere in science-related literature. For 65
years mainstream sources have been spouting baloney and incorrect or
misleading information on this topic.
The
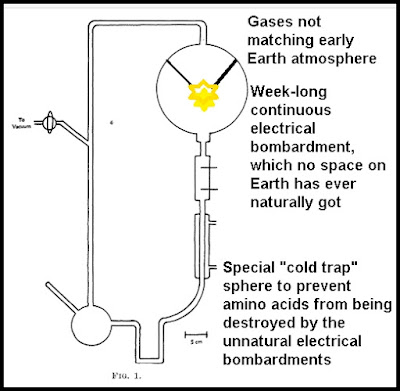
Miller-Urey experiment used a glass apparatus with several different
glass chambers connected by tubes. The top glass chamber was filled
with a mixture of gases consisting mainly of ammonia and methane.
This chamber had an electrical spark unit that continually bombarded
these gases with electricity. In his original paper Miller stated, "The discharge was run continuously for a week." If you imagine the electrical sparks
coming from a half-severed power line, you will get an idea of how
this electrical spark unit worked. The lower chamber consisted of very warm water. After a week of electrical discharges delivered to the gases,
amino acids were found in the water of the lower chamber.
For decades this
experiment was hailed as something that had shown that
“building blocks of life could naturally form,” or that before life appeared there once existed on Earth some "primordial soup" rich in such "building blocks of life." Over the next 65
years, this phrase of “building blocks of life” was constantly
used in discussions of the Miller-Urey experiment. But it was never
an accurate or appropriate term to be using to describe the amino
acids that were produced. The real building blocks of visible
organisms are cells, which are built up from the building blocks of
protein molecules. The real building blocks of a microscopic microbe
are protein molecules, chemical units that usually consist of
hundreds of amino acids arranged in just the right way. Amino acids
are merely the building blocks of the building blocks of one-celled
organisms, and are merely the building blocks of the building blocks
of the building blocks of human beings. So it was never accurate to
be calling amino acids “building blocks of life.” Calling an
amino acid a “building block of life” is as misleading as calling
a tiny clay speck “a building block of a house.” Such clay specks
are merely the building blocks of a brick, which is a building block
of a house.
There
is another reason why it is a very misleading analogy to describe
amino acids as “building blocks of life.” A building block can be
used in any order. If I have a dump truck dump a huge pile of bricks
on the lot of my construction site, I can use those bricks in any
order to create a brick wall that is the beginning of a house. But
amino acids are very different. To make some functional protein,
amino acids must be added in just the right order. Shuffle the amino
acid sequence of a protein molecule, and you will destroy its
functionality. A good and fair analogy would be to compare a protein
molecule to an ordered and fine-tuned sequence such as the ordered
sequence of characters that make up an essay, a chapter, or a
computer program. An amino acid can then be compared to a particular
character in such a sequence. Rather than using such a good analogy
(appropriate for a case that requires a special arrangement that is
an ordered fine-tuned sequence), the science literature has for 65
years used an inappropriate and misleading analogy in which amino
acids are compared to building blocks (things that do not require
some special arrangement).
Very few of the countless discussions of the Miller-Urey experiment clearly stated the important fact that the experiment had produced
amino acids with an equal mixture of right-handed and left-handed
amino acids, unlike what is found in earthly organisms. An article in Astrobiology magazine puts it this way:
“A
curious aspect of Earth’s life forms is that they contain (with few
exceptions) only left-handed amino acids. In contrast, when
scientists synthesize amino acids from nonchiral precursors, the
result is always a 'racemic' mixture – equal numbers of right- and
left-handed forms. Scientists have been unable to perform any
experiment that, when starting with conditions believed to emulate
those of early Earth, results in a near-total dominance of
left-handed amino acids, says George Cody, a geochemist at the
Carnegie Institute of Washington.”
Once
the Miller-Urey experiment occurred, the world of science literature
began to repeat again and again the claim that such an experiment had
shown that there must have been some “primordial soup” filled
with amino acids. In fact, the experiment actually provided no
warrant for any such claim. This is because the experiment had
involved week-long continuous electrical bombardment of gases,
something that has never occurred in the history of planet Earth.
There
is no reason to believe that lightning was any more common in the
early Earth than it is today. The chance of someone being hit by
lightning is about 1 in 700,000 per year. The chance of a particular
man-sized spot being hit twice by lightning in the same year is
about 1 in 14,000,000,000,000. But the Miller-Urey experiment used
an electrode to provide continuous electricity for a week.
During that week, very many thousands of electrical jolts were
transmitted into the apparatus. In the history of Earth there has
never been any area that got even a millionth of that frequency of
electrical stimulation from natural lightning, which lasts for only about 30 millionths of a second when it strikes. The length of electrical stimulation in the Miller-Urey experiment was about 20 billion times longer than the length of time that any natural spot on Earth would have been electrically stimulated by lightning. This by itself is
sufficient reason for saying that the Miller-Urey experiment was not
a realistic simulation of early Earth conditions. This huge problem
with the experiment was ignored by 99% of the treatments of the
Miller-Urey experiment in science literature.
Another reason for doubting the relevancy of the Miller-Urey results is that the electricity was created in a closed glass apparatus chamber. Natural lightning is never created in such a closed environment, but arises instead in the open air, where there is ample opportunity for dissipation of the energy.
The extreme rarity of amino acids outside of living organisms was another reason for thinking that there could not be any natural non-biological chemistry by which amino acids are created in appreciable amounts, contrary to what the Miller-Urey experiment may have suggested. As a scientist named Menez stated, "People have predicted the existence of abiotic amino acids from experiments and thermodynamic calculations, but no one has seen them occurring in terrestrial settings, neither in ponds nor in rocks."
Another reason for doubting the relevancy of the Miller-Urey results is that the electricity was created in a closed glass apparatus chamber. Natural lightning is never created in such a closed environment, but arises instead in the open air, where there is ample opportunity for dissipation of the energy.
The extreme rarity of amino acids outside of living organisms was another reason for thinking that there could not be any natural non-biological chemistry by which amino acids are created in appreciable amounts, contrary to what the Miller-Urey experiment may have suggested. As a scientist named Menez stated, "People have predicted the existence of abiotic amino acids from experiments and thermodynamic calculations, but no one has seen them occurring in terrestrial settings, neither in ponds nor in rocks."
Then
there is the issue of the type of gases used in the Miller-Urey
experiment. The two scientists used the wrong mixture of gases. They
tried to simulate the early earth's atmosphere by using mainly ammonia and
methane. But there never was any sound basis for thinking that such
gases were the main gases in the early Earth's atmosphere. It is now
believed that the early earth's atmosphere was mainly carbon dioxide, nitrogen and water vapor.
A
1965 scientific paper makes clear that there was no basis in that time for
thinking that the early earth's atmosphere was mainly methane,
ammonia or any mixture of the two. The paper tells us, “The growth
of the initial atmosphere and oceans from volcanic discharge seems
probable.” The paper then lists some of the contents of volcanic
discharges, giving these numbers:
Water
vapor: 20-97%
Carbon
dioxide: 1-40%
Nitrogen
(N2) : 1-38%
Sulfur
dioxide: 0-8%
Hydrogen:
0-4%
Chlorine:
0-4%
The
paper also says that methane and ammonia are only emitted by
volcanoes in “small quantities.”
Anyone
putting such facts together in a kind of “two plus two equals four”
way should have realized that it made no sense to assume that the
early earth's atmosphere was mainly methane and ammonia. If the
earth's atmosphere came mainly from volcanoes, then we clearly should
assume that the early earth's atmosphere was mainly the type of gases
most commonly emitted by volcanoes (nitrogen, carbon dioxide, water vapor and sulfur dioxide), and
not some gases such as methane and ammonia that are emitted by
volcanoes only in “small quantities.”
The
facts listed above in the 1965 paper were well known by 1950. So the
scientific basis for not believing that the earth's early atmosphere
was mainly ammonia
and methane was well known by 1950, years before the Miller-Urey
experiment. But once the Miller-Urey experiment was done in the
1950's, the world of science literature ignored such very clear
reasons for thinking the experiment was of no great relevance. A
thousand books and articles hailed the Miller-Urey experiment. Almost all
of these writers of these treatments seemed to throw away their
critical faculties when dealing with this topic. The writers ignored
one very clear and obvious reason for regarding the experiment as
irrelevant (the fact that no place on Earth gets anything even a millionth as much as a week of continuous exposure to lightning). They also
ignored another clear and obvious reason for rejecting the
experiment, that it used the wrong mixture of gases to simulate the
early Earth. For 40 years the experts and writers describing the
Miller-Urey experiment in enthusiastic tones were like some car buyer
who enthusiastically buys a snazzy shiny car, failing to notice heavy smoke and loud
noise coming from the engine during the test drive.
Eventually
more and more evidence piled up that the gases used by Miller and
Urey were not the right mixture. It became more and more evident that
the early Earth's atmosphere was a totally different mixture, one
corresponding pretty closely to actual outputs of volcanoes (a
mixture of mainly nitrogen and carbon dioxide, along with
considerable water vapor and sulfur dioxide).
A 2011 press release preserved on a NASA site states the following: "We can now say with some certainty that many scientists studying the origins of life on Earth simply picked the wrong atmosphere,' said Bruce Watson, Institute Professor of Science at Rensselaer." The "many scientists" referred to include Miller and Urey. The press release tells us that the correct atmosphere (derived from a study of volcanic emissions) would have been "an atmosphere dominated by the more oxygen-rich compounds found within our current atmosphere — including water, carbon dioxide, and sulfur dioxide." A 2007 scientific paper says, "the early Earth is likely to have had a CO2-rich atmosphere, and not a ‘Milley–Urey'’ atmosphere, since at least 4 Ga [4 gigayears] (Canil, 1997; Delano, 2001; Kasting and Catling, 2003)."
Dragging their heels as long as they could, mainstream authorities finally began to eventually let us know (around the year 2010 or so) that the Miller-Urey experiment used the wrong mixture of gases the simulate the early Earth's atmosphere. But they only let us know such a thing decades after they should have told us about this shortcoming.
A 2011 press release preserved on a NASA site states the following: "We can now say with some certainty that many scientists studying the origins of life on Earth simply picked the wrong atmosphere,' said Bruce Watson, Institute Professor of Science at Rensselaer." The "many scientists" referred to include Miller and Urey. The press release tells us that the correct atmosphere (derived from a study of volcanic emissions) would have been "an atmosphere dominated by the more oxygen-rich compounds found within our current atmosphere — including water, carbon dioxide, and sulfur dioxide." A 2007 scientific paper says, "the early Earth is likely to have had a CO2-rich atmosphere, and not a ‘Milley–Urey'’ atmosphere, since at least 4 Ga [4 gigayears] (Canil, 1997; Delano, 2001; Kasting and Catling, 2003)."
Dragging their heels as long as they could, mainstream authorities finally began to eventually let us know (around the year 2010 or so) that the Miller-Urey experiment used the wrong mixture of gases the simulate the early Earth's atmosphere. But they only let us know such a thing decades after they should have told us about this shortcoming.
Of
the experiments using a more suitable mixture of gases to simulate
the early Earth's atmosphere, it must be said that none of them have
produced a variety of amino acids under conditions realistically
simulating the early Earth. In general the methodology of such
“Miller-Urey sequel experiments” has been just as objectionable
as the Miller-Urey experiment. An example is an experiment that
subjected gases to 2 hours of intense proton bombardment. No area on
Earth ever received so high a dose of radiation. Another example is
an experiment that used strong electrical charges to produce amino
acids. Such charges would not have been available in the early
Earth.
The
situation now is that our mainstream authorities will typically let
us know that the Miller-Urey experiment used the wrong gases to
simulate the early Earth. But they will typically make such a
confession somewhere where it is least likely to be noticed by the
reader. It's as if our mainstream writers were still trying to
squeeze as much effect from the Miller-Urey experiment as they can,
even though the experiment has been debunked. A typical treatment
will go like this:
- The Miller-Urey experiment will be discussed in a way that initially leads the reader to think that it was something indicating that there would have been many amino acids on the early Earth.
- Somewhere much later in the discussion, it will be mentioned that the Miller-Urey experiment did not use a correct mixture of gases.
Of
course, this type of treatment is misleading.
It's as misleading as a blog post that tells you in paragraph one
that a certain Senator has been accused of murder, and then tells you
in paragraph ten that the person making the claim about the murder has
admitted that he was merely joking or playing a prank.
An
example of this type of treatment is in the Wikipedia.org article on
abiogenesis. Near the beginning of the article, we read a statement
designed to make the reader think that the Miller-Urey experiment
told us something important: “The classic 1952 Miller–Urey
experiment and similar research demonstrated that most amino acids,
the chemical constituents of the proteins used in all living
organisms, can be synthesized from inorganic compounds under
conditions intended to replicate those of the early Earth.” Only
much, much later in the article do we read about how the Miller-Urey
experiment used the wrong mixture of gases to simulate the early
earth's atmosphere. It's as if some rule was in operation that our
mainstream authorities are still trying to make as many people as
possible think that the Miller-Urey experiment helped bolster the
idea of a natural origin of life, and that information debunking the
experiment must be buried where it is least likely to be noticed.
And similarly, a cigarette manufacturer may have 95% of its ad
telling you how great its cigarettes are, and only put at the bottom
a little box telling you that cigarettes cause cancer.
Then
there are the mainstream sources that claim that it doesn't
matter that the Miller-Urey experiment used the wrong mixture of
gases to simulate the early Earth's atmosphere, on the grounds that
similar experiments using the correct mixture have produced similar
results. Such claims are about as accurate as someone claiming that
it doesn't matter that he got fired from his job, on the grounds that
he has “similar methods of producing revenue,” while referring to
things such as gathering bottles for cash or begging for money on the
street. There has been no experiment realistically simulating early
Earth conditions that produced any of the twenty amino
acids.
An
example of the extremely misleading treatments of the Miller-Urey
experiment that we continue to see in the science literature can be
found in the recent book Imagined Life by scientists James
Trefil and Michael Summers. Here is a statement on page 38 of their
book, a statement that is filled with erroneous claims. I
will discuss its errors after I quote it.
“Miller-Urey-type
experiments have produced virtually every important molecule found in
living systems, including stretches of DNA and protein molecules. And
surprisingly, even though the consensus is that Miller and Urey had
the wrong atmospheric composition in their experiment, it just
doesn't matter. Experiments with different atmospheric compositions
and different energy sources have produced essentially the same
results, albeit with different yields, depending upon the assumed
composition of the atmosphere. Furthermore, complex organic molecules
(including amino acids) have been found in meteorites, in
interstellar dust clouds, and even in debris disks which surround
stars and in which exoplanets are forming. Against all expectations, in other words, the basic
molecular building blocks of life are common – in fact, they're all
over the place.”
Let
us carefully examine these statements one by one.
Trefil
and Summers statement #1: “Miller-Urey-type
experiments have produced virtually every important molecule found in
living systems, including stretches of DNA and protein molecules.”
This
is one of the most outrageous falsehoods I have ever
read in any book. Human beings have roughly 20,000
different types of protein molecules.
Not one of them has ever been produced in a “Miller-Urey-type
experiment.” No such experiment has ever produced any protein
molecule. Miller-Urey-type experiments only produce individual amino
acids, and the median number of amino acids in a protein molecule is about 375 amino acids. It is therefore not at all true to say that
Miller-Urey type experiments have produced “stretches” of protein
molecules, the word "stretch" meaning an "area or expanse." No Miller-Urey-type experiment has ever even produced a
nucleotide, which is the basic building block of a DNA molecule (a DNA molecule has billions of nucleotides). So
it is utterly false to say that such experiments have produced “stretches
of DNA.”
Trefil
and Summers statement #2: "And
surprisingly, even though the consensus is that Miller and Urey had
the wrong atmospheric composition in their experiment, it just
doesn't matter. Experiments with different atmospheric compositions
and different energy sources have produced essentially the same
results, albeit with different yields, depending upon the assumed
composition of the atmosphere."
It
certainly does matter very much that Miller and Urey “had the wrong
atmospheric composition in their experiment,” because such a thing
invalidates their whole experiment, making it worthless as a guide to
conditions on the early Earth. As for other types of experiments that
were inspired by the Miller-Urey experiment, they all have a defect
similar to one in the Miller-Urey experiment: they fail to
realistically simulate early Earth conditions. Notice that Trefil and Summers merely vaguely refer to "different atmospheric compositions and different energy sources" rather than giving us the details of some specific experiment that realistically simulated early earth conditions and produced amino acids. They cannot give us such specifics because there has never been such an experiment.
An
example of such "Miller-Urey-type" experiments is the one discussed in this paper by Kobayashi and
others. They subjected a mixture of carbon monoxide, nitrogen and
water to two hours of "high-energy proton irradiation" of 3 million electron volts. This produced spherical
micro-structures which yielded amino acids only after hydolysis with
hydrogen chloride. Such a technique is not at all a realistic
simulation of any conditions on the early Earth. No part of the early
Earth was subjected to anything like two hours of high-energy proton bombardment,
nor did any part of the early Earth undergo hydrolysis with hydrogen
chloride. The authors did not even use a correct mixture of gases
corresponding to the mixture believed to have existed on the early
Earth, for their mixture used carbon monoxide rather than carbon
dioxide. The authors state that a similar proton-bombardment
experiment “did not produce amino acids” when a more realistic
mixture of gases was used, consisting of carbon dioxide, nitrogen and
water.
Another paper sometimes cited as providing "similar results" to the Miller-Urey experiment (but with a realistic mixture of gases) is the paper "Thermochemical Aspects of the Conversion of the Gaseous System CO2->N2->H20 Into a Solid Mixture of Amino Acids” by F. Hanic and others. Such a citation is bogus, because the paper does not describe an attempt to simulate early earth conditions. The method described is quite technological, a technique depending on electrodes and involving a "high voltage, spontaneously pulsing direct current electric discharge system operating in corona discharge geometry." Such a method involves fancy and specific gadgets, something much more complicated than anything that existed on the early Earth.
Another paper sometimes cited as providing "similar results" to the Miller-Urey experiment (but with a realistic mixture of gases) is the paper "Thermochemical Aspects of the Conversion of the Gaseous System CO2->N2->H20 Into a Solid Mixture of Amino Acids” by F. Hanic and others. Such a citation is bogus, because the paper does not describe an attempt to simulate early earth conditions. The method described is quite technological, a technique depending on electrodes and involving a "high voltage, spontaneously pulsing direct current electric discharge system operating in corona discharge geometry." Such a method involves fancy and specific gadgets, something much more complicated than anything that existed on the early Earth.
Trefil
and Summers statement #3: "Furthermore,
complex organic molecules (including amino acids) have been found in
meteorites, in interstellar dust clouds, and even in debris disks
which surround stars and in which exoplanets are forming. Against all expectations, in other
words, the basic molecular building blocks of life are common – in
fact, they're all over the place.”
The
authors refer to meteorites such as the Murchison meteorite. The
claim that amino acids were found in that meteorite (in very small
trace amounts) is disputed. The article here in Astrobiology magazine
refers to scientists who are skeptical about such a claim, and who
suspect that the amino acids detected are due to earthly
contamination. No more than trace amounts of biologically relevant amino acids have been found in meteorites. For example, we read here that "glycine was the most abundant amino acid" found in the Murchison meteorite, and that it was found in an amount of only 3 parts per million.
According to the source here, no more than eight of the
twenty amino acids used by living things have ever been reported as
being detected in meteorites. The traces of amino acids claimed to
be deep in the large Murchison meteorite and similar meteorites are
biologically irrelevant. Life couldn't start in the dry inside of a
meteorite, and if a meteorite broke up catastrophically, any tiny traces of amino acids in it would probably be destroyed. Only
one of the 20 amino acids used by living things has been found in an
interstellar dust cloud: glycine, the simplest amino acid. The
“basic molecular building blocks of life” are proteins, and no
protein has ever been detected in outer space. There is no
appreciable trace of 19 out of 20 amino acids in outer space. So it
was misleading for Trefil and Summers to have said (referring to outer space), “the basic molecular building
blocks of life are common – in fact, they're all over the place.”
After telling us on page 38 that "Miller and Urey had the wrong atmospheric composition in their experiment," Trefil and Summers on page 95 say, "We described the Miller-Urey experiment, which showed that ordinary chemical processes in Earth's atmosphere could generate the basic molecular building blocks of life." This is what goes on in the science literature these days: make it look in one place that the Miller-Urey experiment proved something terribly important, but confess in some other place that the experiment had an invalidating defect. The statement on page 95 by Trefil and Summers was as false as their mythical claim on page 47 that "DNA contains the 'blueprint' of the living thing in which it is found." DNA merely contains low-level chemical information such as the amino acid sequence of proteins, and (as discussed here) DNA does not contain anything like a blueprint or recipe or algorithm for building either a complete body or any organ or appendage of a body. DNA does not even specify how to make any of the 200 types of cells in the human body, nor does it even specify how to make any of the organelles of such cells.
So many faulty claims have been discussed or quoted here that the facts should be concisely summarized:
(1) Amino acids are not found in the natural world in appreciable amounts outside of living things. As scientist Menez stated, "No one has seen them occurring in terrestrial settings, neither in ponds nor in rocks."
(2) No scientific experiment realistically simulating the early Earth has ever produced any of the 20 amino acids used by living things, with the exception of experiments (such as this experiment) producing glycine or alanine (the two simplest amino acids) at trace levels of 40 parts per million, or even smaller amounts. Except for the experiment producing only trace amounts of glycine or alanine, the only experiments attempting to produce amino acids have had one or more major defects, such as not using a realistic mixture of gases to simulate the early Earth's atmosphere, or exposing a sample of gas to utterly unrealistic energy exposures (such as continuous one-week electricity bombardments or 2-day proton beam bombardments) that no area on Earth would have been subjected to.
(3) The famous Miller-Urey experiment was guility of three such defects: using an inappropriate mixture of gases to simulate the early Earth's atmosphere; exposing such gases to continuous week-long electricity bombardments many millions of times longer than any spot on Earth would endure from a lightning bolt; and using a glass chamber to confine electricity in a way unlike anything that would occur naturally.
(4) The Miller-Urey experiment did not actually produce amino acids such as found in living things (all left-handed), but instead a mixture in which right-handed amino acids were as common as left-handed amino acids.
(5) Although accounts of the Miller-Urey experiment typically described amino acids as "building blocks of life," the actual building blocks of microscopic life are proteins, things which typically require extremely specially-ordered arrangements of hundreds of amino acids (unlike houses which do not require that building blocks be used in some special order).
(7) There is no geological, astronomical or meteorological reason for thinking that amino acids existed in anything other than negligible amounts before life existed, and there is no evidential basis for believing that there ever existed any such thing as a prebiotic "primordial soup" that was rich in either amino acids or the building blocks of DNA (nucleotides).
For 65 years the mainstream science literature has had coverage of the Miller-Urey experiment that has largely been baloney. Very sadly, the coverage of the Miller-Urey experiment in scientific literature suggests that scientists and science writers will sometimes hype up a misleading pile of runaway praise and inappropriate accolades relating to evidence or arguments or experiments with very glaring defects, when such work seems to offer some result that seems to support some dogma that scientists eagerly wish to believe.
The Miller-Urey apparatus included a special "cold trap" that isolated the amino acids created from being disrupted by the energy source. Such a thing does not correspond to anything that existed on the early Earth. You might realistically simulate Earth conditions by having an outdoor apparatus the size of an Olympic-sized swimming pool, filled with millions of gallons of water. By having the apparatus outside, you would simulate actual pond conditions, in which water is partially replaced each month by rainfall and evaporation. With such an experiment, there would never be any concentration of amino acids, and no liter of water would ever have any more than microscopic traces of amino acids.
A NASA page tells us an additional reason why the Miller-Urey experiment never was a realistic simulation of early Earth conditions. The early Earth was much colder than it is today, because the sun's radiation was much weaker. It is estimated that billions of years ago, the sun's radiation was only 70% of what it is today. What is called the faint young sun paradox is the discrepancy between the weakness of solar radiation billions of years ago and claims that life arose billions of years ago. The NASA page says, "Lightning, which comes from thunderclouds formed by rising warm air, would have been rarer under a 30% dimmer Sun." I explain above why "The length of electrical stimulation in the Miller-Urey experiment was about 20 billion times longer than the length of time that any natural spot on Earth would have been electrically stimulated by lightning." Such a calculation was made before even considering that lightning would have been much rarer in a colder Earth.